4.2. Cas de deux échantillons
Ce type de test est utile lorsque l'on veut établir si deux traitements sont différents ou si un traitement est "meilleur" qu'un autre. Dans tous les cas, le groupe qui a subi le traitement est comparé à celui qui n'en a pas subi, ou qui a subi un traitement différent. Ce cas se présente, par exemple, quand on compare deux méthodes de mesure en soumettant à ces deux méthodes les mêmes individus, choisis dans une population donnée : à chacune des méthodes correspond alors une population de mesures, mais ces populations et les échantillons que l'on peut en extraire, ne sont pas indépendants. Il est aussi possible de soumettre les mêmes sujets à deux traitements différents. Chaque sujet est alors utilisé comme son propre contrôle et il suffit alors de contrebalancer l'effet d'ordre des traitements. Une dernière façon de faire consiste à apparier des sujets et d'assigner aléatoirement les membres de chaque paire aux deux conditions. Cet appariement est toujours délicat. Il faut sélectionner pour chaque paire les sujets les plus semblables possibles par rapport aux variables étrangères qui pourraient affecter le résultat de la recherche entreprise. En effet, dans de telles comparaisons
de deux groupes appariés, des différences significatives peuvent être observées qui ne sont pas le résultat du traitement. Par exemple, la différence observée entre deux méthodes d'apprentissage par deux groupes d'étudiants peut ne pas traduire une
efficacité relative de ces deux méthodes, car d'autres variables (les étudiant d'un groupe sont plus capables ou plus motivés que ceux de l'autre groupe) créent des différences dans les performances. Or nous ignorons ou connaissons mal les variables étrangères pertinentes. Aussi, la qualité de cette deuxième méthode dépend de l'habilité du chercheur, et cette dernière est toujours limitée.
La méthode paramétrique usuelle pour analyser les données de échantillons non indépendants est le test de t, dont nous avons exposé les contraintes. Si nous ne pouvons ou ne voulons pas accepter ces dernières ou si les mesures ne sont pas réalisées, au moins, dans une échelle d'intervalle, nous devons choisir parmi les tests non paramétriques possibles : test de McNemar de la signification de changements, test du signe, test de rang de Wilcoxon, test de Walsh, et le test de randomization pour échantillons appariés.
4.2.1. Échantillons appariés
4.2.1.1. Test des signes (Sign test)
Il s'applique au cas de deux échantillons associées par paires. Il tire son nom du fait qu'il utilise les signes + et -, au lieu de données quantitatives. Il est particulièrement utile dans les cas où il n'est possible que de ranger l'un par rapport à l'autre les membres de chaque paire. Il est basé uniquement sur l'étude des signes des différences observées entre les paires d'individus, quelles que soient les valeurs de ces différences. Les seules contraintes de ce test sont que la variable considérée
ait une distribution continue et que les deux membres de chaque paire sont appariés.
Méthode
L'hypothèse nulle peut s'écrire
P (+) = P (-) = 1/2
P (+) = la probabilité d'observer une différence positive
P (-) = la probabilité d'observer une différence négative.
Lorsque l'hypothèse nulle est vraie et pour N paires d'observations, le nombre de différences positives (ou négatives) est une variable binomiale de paramètres P = Q = 1/2 et N. Le test permet de comparer, grâce à cette distribution, le nombre observé de signes plus (ou moins) et le nombre attendu N/2. Quand certaines différences
sont nulles, les paires d'observations correspondantes sont écartées de l'analyse et la valeur de N est réduite en conséquence.
Petits échantillons
Lorsque N < 25, la table 3 donne les probabilités associées des valeurs x obtenues, sous H0. x
= le nombre des signes les moins fréquents. Le test des signes peut être unilatéral lorsque l'on prédit quel signe + ou - sera le plus fréquent ou bilatéral lorsque les fréquences des deux signes seront simplement différentes.
Exemples
- Vingt paires sont observées; 16 présentent une différence (+) et les 4 autres une différences (-). Donc N = 20 et x = 4.
- Si H1 prédit que les signes + sont les plus fréquents (unilatéralité), la Table 3 révèle que la probabilité d'obtenir la distribution est de 0,006 et que l'on peut rejeter H0 au seuil 0,001. Si H1 prédit simplement que la différence entre les fréquences des deux signes est différente (bilatéralité), il faut doubler la valeur p de la table 3. Dans notre cas, p = 0,012 et H0 ne peut être rejetée au seuil 0,001.
- Douze arbres sont mesurés alors qu'ils sont debout, par une mesure trigonométrique. Puis les mêmes arbres sont mesurés au sol, après abattage. La première méthode donne-t-elle des résultats significativement trop faibles ou trop élevés ?
H0 Il n'y a pas de différences entre les mesures obtenus par la première et la seconde méthodes. H1 il y a une différence significative. Seuil de signification a = 0,05.
Les hauteurs obtenues (en mètres) sont les suivantes :
| Arbres debouts | Arbres abattus | Différences
|
|---|
| 20,4 | 21,7 | -1,3
|
|---|
| 25,4 | 26,3 | -0,9
|
|---|
| 25,6 | 26,8 | -1,2
|
|---|
| 25,6 | 28,1 | -2,5
|
|---|
| 26,6 | 26,2 | 0,4
|
|---|
| 28,6 | 27,3 | 1,3
|
|---|
| 28,7 | 29,5 | -0,8
|
|---|
| 29,0 | 32,0 | -3,0
|
|---|
| 29,8 | 30,9 | -1,1
|
|---|
| 30,5 | 32,3 | -1,8
|
|---|
| 30,9 | 32,3 | -1,4
|
|---|
| 31,1 | 31,7 | -0,6
|
|---|
N = 12 (nombre de différences non nulles) x = 2
La table 3 révèle que pour N = 12, la probabilité (bilatérale) d'obtenir un tel x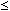 
2 est de (0,019) x 2 = 0,038. L'identité des résultats obtenus par les deux méthodes
de mesure doit être rejetée au seuil de signification 0,05.
Grands échantillons
Lorsque N > 25, on peut utiliser l'approximation normale en faisant intervenir une correction de continuité. Il suffit de calculer la valeur
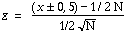
| (5)
|
où x + 0,5 est utilisé lorsque x < 1/2 N et x - 0,5 lorsque x > 1/2 N. La signification d'un tel z peut être déterminée par référence à la table 1. Cette table donne la probabilité unilatérale d'obtenir des valeurs aussi extrêmes que le z
observé. Pour un test bilatéral, la probabilité donnée par la table 1 doit être doublée.
Exemples
- Si l'on reprend l'exemple de comparaison des mesures des arbres, l'approximation normale donnerait :
z = ((2 + 0,5) - 6) / 0,5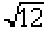 
= 3,5 / 1,7320508 = 2,02
- La table 1 révèle que pour z = 2,02, la probabilité bilatérale associée est (0,0217) x 2 = 0,0434.
Cette valeur conduirait à rejeter l'hypothèse nulle au seuil 0,05. Bien que les échantillons ne contiennent chacun que douze individus, l'approximation est déjà très satisfaisante puisqu'elle donne p = 0,0434 au lieu de p = 0,038.
- Supposons qu'un chercheur veuille déterminer si la vision d'un film sur la délinquence juvénile change les opinions des membres d'une communauté sur la sévérité des sanctions à donner à des délinquents juvéniles. Il extrait un échantillon aléatoire de 100 adultes de la communauté. Chaque sujet sera son propre contrôle. Il leur demande de prendre position sur la sévérité plus ou moins grande des punitions à infliger
aux délinquents juvéniles. Il leur présente ensuite le film et réitère sa question après.
Hypothèse nulle
- H0 : le film n'a pas d'effet sur l'opinion des sujets. H1 : le film a un effet systématique.
Test statistique
- Le test des signes est choisi pour cette étude portant sur deux groupes appariés et dont les mesures sont réalisées dans l'échelle ordinale. Les différences pourront être représentées par des plus ou des moins.
Niveau de signification
- Posons a = 0,01 ; N = le nombre de sujets qui change d'opinion, quel qu'en soit le sens.
Distribution d'échantillonnage
- N > 25 aussi z est calculé avec la formule (5) et la Table 1 donne la probabilité associée aux valeurs aussi extrêmes que le z obtenu.
Région de rejet
- Comme H1 ne prédit pas la direction des différences, la région de rejet est bilatérale.
Décision
- Les résultats de cette étude fictive sont les suivants :
| | Opinion avant le film
|
|---|
| | Moins | Plus
|
|---|
| Opinion après le film | Plus | 59 | 7
|
|---|
| Moins | 8 | 26 |
- Ces données montre que 15 adultes (8 + 7) n'ont pas été affecté par la vision du film et 85 l'ont été. Si le film n'a pas d'effet systématique, nous nous attendrions à ce que à peu près la moitié de ceux qui ont modifié leur jugement entre avant et après a changé de plus à moins et à peu près la moitié a changé de moins à plus. Soit 42,5
sujets auraient modifié leur jugement dans un sens ou dans l'autre.
x = 26; N = 85 donc x < 1/2 N
z = ((26 + 0,5) - 42,5) / 0,5 (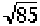
) = 16 / 4,609772 = 3,47
- Par référence à la Table 1, p
= 2 (0,0003) = 0,0006 < a = 0,01
Nous pouvons rejeter l'hypothèse nulle. Nous pouvons conclure, dans cette étude fictive, que la vision du film a eut un effet significatif sur l'opinion des adultes concernant la sévérité des peines à infliger aux délinquents juvéniles.
4.2.1.2. Test des rangs appliqué au cas d'échantillons appariés (Wilcoxon matched-pairs signed-ranks test)
Le test précédent n'utilise que l'information sur la direction des différences entre paires. Si nous pouvons prendre en compte en plus la grandeur des différences, un test plus puissant peut être utilisé. Le test de Wilcoxon donne plus de poids à une paire qui montre une large différence entre les deux conditions qu'à une paire ayant une
faible différence. Cela implique que l'on puisse dire quel membre d'une paire est plus grand que l'autre (donner le signe de la différence), mais aussi que l'on puisse ranger les différences en ordre croissant.
Méthode
di = différence entre chaque paire, représentant la différence entre les scores appariés obtenus lors des deux traitements. Chaque paire a un di.
Ranger tous les di sans tenir compte de son signe. Dans ce cas, lorsque l'on range les di, un di de -1 est affecté d'un rang inférieur à celui d'un di de -2 ou +2. Puis réaffecter à chaque rang le signe de la différence.
Si les traitements A et B sont équivalent, donc si H0 est vraie, la somme des rangs ayant un signe positif et celle des rangs ayant un signe négatif devraient être à peu près égale. Mais si la somme des rangs de signes positifs est très différente de celle des rangs de signes négatifs, nous en déduirons que le traitement A diffère du traitement B, et rejèterons l'hypothèse nulle. Donc, il y a rejet d'H0 que la somme des rangs de signe négatif ou que celle des rangs de signe positif soit faible.
Il est possible que les deux scores d'une quelconque paire soient égaux. Il n'y a pas de différence observée entre les deux traitements pour cette paire (d = 0). De telles paires sont abandonnées. N est alors égal au nombre de paires dont la différence entre les traitements n'est pas nulle. Mais deux ou plus des différences observées entre paire peuvent être égales entre elles. On donne alors le même rang
à ces valeurs liées. Le rang affecté est la moyenne des rangs qu'auraient eu les diverses valeurs si elles avaient différées. Ainsi, trois des paires observées présentent les différences suivantes : -1, -1 et +1. Chaque paire aura le rang 2, car (1 + 2 + 3) / 3 = 2. La différence suivante aura alors le rang 4, puisque les rangs 1, 2, et 3 ont déjà été utilisé.
Petits échantillons
T = la somme des rangs du signe observée le moins fréquent. La table 5 donne les valeurs critiques de T et leurs niveaux de signification associés pour N 25. Si le T observé est égal ou inférieur à la valeur donnée dans la table pour un niveau de signification et pour le nombre de différences non nulles N, l'hypothèse nulle peut être rejetée à ce niveau de signification.
Exemples
- Un psychologue de l'enfance veut tester l'effet de l'assistance à l'école maternelle sur la compréhension sociale des enfants. Il estime cette compréhension à partir des réponses que les enfants donnent à une série de questions portant sur des images
représentant diverses situations sociales. Chaque enfant obtient ainsi un score compris entre 0 et 100. Le psychologue ne peut pas affirmer que les différences observées entre scores sont numériquement exactes (il ne peut pas dire qu'un score de 60 est le double d'un score de 30, ni que la différence entre 60 et 40 est exactement le double de la différence entre 40 et 30). Cependant, il pense que les scores sont suffisamment précis pour qu'il puisse les ranger selon leur valeur absolue. Pour tester l'effet de l'assistance à l'école maternelle sur la compréhension sociale des enfants, il utilise 8 paires de jumeaux. L'un des jumeaux est envoyé à l'école, alors que l'autre reste à la maison pendant un trimestre. L'affectation se faisant au hasard. A la fin du
trimestre, il estime la compréhension sociale de chacun des enfants.
L'hypothèse nulle : il n'y pas de différence entre la compréhension sociale des enfants resté à la maison et celle des enfants ayant suivi l'école.
Les résultats sont donnés dans le tableau ci-dessous.
| Paires | Score enfants scolarisés | Score enfants Non scolarisé | d | Rang de d | Rang avec le signe le - fréquent
|
|---|
| a | 82 | 63 | 19 | 7 |
|
|---|
| b | 69 | 42 | 27 | 8 |
|
|---|
| c | 73 | 74 | -1 | -1 | 1
|
|---|
| d | 43 | 37 | 6 | 4 |
|
|---|
| e | 58 | 51 | 7 | 5
|
|---|
| f | 56 | 43 | 13 | 8 |
|
|---|
| g | 76 | 80 | -4 | -3 | 3
|
|---|
| h | 65 | 62 | 3 | 2 |
|
|---|
| | | | | T = 4 |
|---|
La table 5 montre que pour N = 8, un T = 4 nous permet de rejeter l'hypothèse nulle au seuil 0,05 pour un test bilatéral. Par conséquent, nous conclurions, dans cette étude fictive, que l'expérience de l'école affecte la compréhension sociale des enfants.
Ces données sont aussi traitables par le test des signes. Dans ce cas, x = 2 et N = 8, la Table 3 montre que p
= (0,145) 2 = 0,290 et nous ne pourrions pas rejeter H0 au seuil 0,05.
Grands échantillons
Lorsque N est supérieur à 25, il peut être démontré que la somme des rangs T est pratiquement
normale et que l'on peut calculer
z = (T - (N (N +1) /4)) / 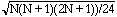 | (6) |
et se référer à la Table 1.
Pour montrer la précision de l'approximation, nous pouvons traiter les données précédentes N = 8, T = 4,
z = (4 - ((8) (9))/4) /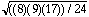
= - 1,96
La Table 1 révèle que pour z = -1,96, p
= (0,025) 2 = 0,05, c'est-à-dire la même probabilité qu'en utilisant la table des valeurs critiques de T.
Exemple
- Si l'on demande à des prisonniers de choisir entre deux jeux leur permettant de perdre ou de gagner des cigarettes, il est possible à un expérimentateur de prédire le choix qui sera fait par chaque sujet dont on connait la valeur subjective qu'il accorde aux cigarettes. Mais dans certains cas, la prédiction est hasardeuse lorsque les termes du choix proposé au sujet sont soit également attractifs ou également peu attractifs. Cependant, dans ces cas, le temps s'écoulant entre la proposition et le choix du sujet risque de s'allonger. Aussi l'expérimentateur peut-il faire l'hypothèse que
les latences de réponse pour les choix imprévisibles seront plus longues que celles pour les choix prévisibles.
- Une différence fut obtenu pour chaque sujet en soustrayant son temps médian de réponse dans le cas des décisions correctement prédites de celui des décisions incorrectement prédites.
Les résultats obtenus pour trente prisonniers sont donnés dans la table ci-dessous.
| Prisonnier | d | Rang d | Rang du signe le - fréquent
|
|---|
| 1 | -2 | -11,5 | 11, 5
|
|---|
| 2 | 0 | |
|
|---|
| 3 | 0 | |
|
|---|
| 4 | 1 | 4,5 |
|
|---|
| 5 | 0 | |
|
|---|
| 6 | 0 | |
|
|---|
| 7 | 4 20,0
| | 8 | 4 | 20,0 |
|
|---|
| 9 | 1 | 4,5 |
|
|---|
| 10 | 1 | 4,5 |
|
|---|
| 11 | 5 | 23,0 |
| | 12 | 3 | 16,5 |
|
|---|
| 13 | 5 | 23,0 |
|
|---|
| 14 | 3 | 16,5 |
|
|---|
| 15 | - 1 | - 4,5 | 4,5
|
|---|
| 16 | 1 | 4,5
|
|---|
| 17 | - 1 | - 4,5 | 4,5
|
|---|
| 18 | 5 | 23,0 |
|
|---|
| 19 | 8 | 25,5 |
|
|---|
| 20 | 2 | 11,5 |
|
|---|
| 21 | 2 | 11,5 |
|
|---|
| 22 | 2 | 11,5 |
|
|---|
| 23 | -3 | -16,5 | 16,5
|
|---|
| 24 | -2 | -11,5 | 11,5
|
|---|
| 25 | 1 | 4,5 |
|
|---|
| 26 | 4 | 20,0 |
|
|---|
| 27 | 8 | 25,5 |
|
|---|
| 28 | 2 | 11,5 |
|
|---|
| 29 | 3 | 16,5 |
|
|---|
| 30 | -1 | - 4,5 | 4,5
|
|---|
| | | T = 53,0 |
|---|
|
|---|
N = 26 , quatre différences étant nulles.
z = ((53 - (26) (27)) / 4) /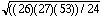
= -3,11
La Table 1 montre que pour un z = -3,11, p = 0,0009, car le test est unilatéral puisque la direction de la différence est prédite. p < a = 0,01, nous pouvons donc rejeter H0. Nous concluons que les latences des décisions incorrectement prédites sont significativement supérieure à celle des décisions correctement prédites.
Discussion
Le test de McNemar peut être utilisé lorsque les données sont mesurées dans l'échelle nominale. Il n'a pas d'équivalent dans le cas de deux échantillons appariés.
Si le score de l'un des membres d'une paire peut être déclaré "plus grand" que le score de l'autre membre de la même paire (échelle ordinale), le test des signes est applicable.
Quand les mesures sont réalisées dans une échelle ordinale à la fois dans les paires et entre elles, le test de Wilcoxon doit être utilisé.
Le test de Walsh est applicable à de petits échantillons (N < 15) quand il est possible d'affirmer que les échantillons observées proviennent de populations symétriques et continues et que les données sont mesurées dans une échelle d'intervalle.
Le test de randomization n'est applicable que lorsque N est suffisamment petit et
que les mesures sont, au moins, dans une échelle d'intervalle. Ce test prend en compte toute l'information des échantillons et il est donc aussi efficace qu'un test de t.
