Introduction aux Statistiques
Citation :
Introduction aux statistiques - © 1996, Ramousse R., Le Berre M. & Le Guelte L.
|
|
L’analyse factorielle des correspondances traite des tableaux de contingence (tableaux de dépendance) dans lesquels un couple (i, j) correspond à un nombre positif kij qui est en général le résultat d’un dénombrement.
Les données de base sont habituellement regroupées dans un tableau. On étudie simultanément, sur une population, deux variables qualitatives I, J pouvant prendre respectivement n et p valeurs (ou modalités). On note kij le nombre d’individus appartenant simultanément aux catégories i et j des variables I et J.
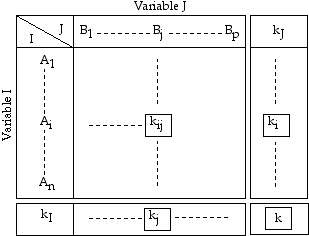
Au tableau kij, sont associés deux tableaux à une dimension chacun : le tableau des marges en ligne kI et le tableau des marges en colonne kJ. L’ensemble tableau de contingence et tableaux marginaux est représenté ci-dessous :
Par exemple : le tableau 10x8 ci-dessous croise 10 catégories socioprofessionnelles avec 8 modes d’hébergements en vacances.
|
|
hôtel
|
locat
|
propri
|
parent
|
amis
|
tente
|
villag
|
divers
|
|
|
|
160
|
28
|
0
|
321
|
36
|
141
|
45
|
65
|
|
| Salariés |
35
|
34
|
1
|
178
|
8
|
0
|
4
|
0
|
|
| Patrons |
700
|
354
|
229
|
959
|
185
|
292
|
119
|
140
|
|
| Cadre sup |
961
|
471
|
633
|
1580
|
305
|
360
|
162
|
148
|
|
| Cadre moy |
572
|
537
|
279
|
1689
|
206
|
748
|
155
|
112
|
|
| Employés |
441
|
404
|
166
|
1079
|
178
|
434
|
178
|
92
|
|
| Ouvriers |
783
|
1114
|
387
|
4052
|
497
|
1464
|
525
|
387
|
|
| Personnels |
65
|
43
|
21
|
294
|
79
|
57
|
18
|
6
|
|
| Autres actif |
77
|
60
|
189
|
839
|
53
|
124
|
28
|
53
|
|
| Non actifs |
741
|
332
|
327
|
1789
|
311
|
236
|
102
|
102
|
|
| Total |
4535
|
3377
|
2232
|
12780
|
1858
|
3856
|
1336
|
1105
|
|
Tableau 1
Dans ce tableau, lignes et colonnes jouent des rôles analogues : ce sont deux partition d’une même population. Pour que les distances entre points-lignes et points-colonnes aient un sens, il faudra faire intervenir les profils des lignes et des colonnes, c-à-d les répartitions en pourcentage à l’intérieur d’une ligne et d’une colonne. En effet, deux observations i et i’ seront considérées comme identiques si les lignes correspondantes sont proportionnelles.
En effet, la distance entre, par exemple, le point " ouvrier " et le point " personnel de service ", calculée à pertir des effectifs bruts du tableau 1, ne ferait que traduire les différences d’effectifs, considérables, entre ces deux catégories. Par contre, calculée sur les profils-lignes du tableau 2, elle traduira les différences de comportement vis-à-vis du mode d’hébergement en vacances, en comparant les pourcentages de chacun de ces modes, sans tenir compte des effectifs totaux des deux catégories. De la même façon, pour comparer deux modes d’hébergements, on consultera les profils socio-professionnels du tableau 3.
On définira donc le tableau des profils de I sur J en posant :
On crée ainsi des profils d’hébergement (profils lignes) : tableau 2 (100 x 
)
|
|
hôtel
|
locat
|
propri
|
paren
|
amis
|
tente
|
villag
|
divers
|
total
|
| Agricult |
20,1
|
3,5
|
0,0
|
40,4
|
4,5
|
17,7
|
5,7
|
8,1
|
100,00
|
| Salariés |
13,4
|
13,1
|
0,4
|
68,5
|
3,1
|
0,0
|
1,5
|
0,0
|
100,00
|
| Patrons |
23,5
|
11,9
|
7,7
|
32,2
|
6,2
|
9,8
|
4,0
|
4,7
|
100,00
|
| Cadre s |
20,8
|
10,2
|
13,7
|
34,2
|
6,6
|
7,8
|
3,5
|
3,2
|
100,00
|
| Cadre m |
13,3
|
12,5
|
6,5
|
39,3
|
4,8
|
17,4
|
3,6
|
2,6
|
100,00
|
| Employés |
14,8
|
13,6
|
5,6
|
36,3
|
6,0
|
14,6
|
6,0
|
3,1
|
100,00
|
| Ouvrier |
8,5
|
12,1
|
4,2
|
44,0
|
5,4
|
15,9
|
5,7
|
4,2
|
100,00
|
| Personnel |
11,1
|
7,4
|
3,6
|
50,4
|
13,6
|
9,8
|
3,1
|
1,0
|
100,00
|
| Autres actif |
5,4
|
4,2
|
13,3
|
59,0
|
3,7
|
8,7
|
3,0
|
3,7
|
100,00
|
| Non actifs |
18,8
|
8,4
|
8,3
|
45,4
|
7,9
|
6,0
|
2,6
|
2,6
|
100,00
|
| Profil marginal de J |
14,6
|
10,9
|
7,2
|
41,0
|
6,0
|
12,4
|
4,3
|
3,6
|
100,00
|
Tableau 2
et des profils socio-professionnels (profils colonnes) : tableau 3 (100 x
)
|
|
hôtel
|
locat
|
propri
|
paren
|
amis
|
tente
|
villag
|
divers
|
|
| Agricult |
3,5
|
0,8
|
0,0
|
2,5
|
1,9
|
3,6
|
3,4
|
5,9
|
2,6
|
| Salariés |
0,8
|
1,0
|
0,0
|
1,4
|
0,4
|
0,0
|
0,3
|
0,0
|
0,8
|
| Patrons |
15,5
|
10,5
|
10,3
|
7,5
|
10,0
|
7,6
|
8,9
|
12,7
|
9,6
|
| Cadre s |
21,2
|
13,9
|
28,4
|
12,4
|
16,4
|
9,3
|
12,2
|
13,4
|
14,9
|
| Cadre m |
12,6
|
15,9
|
12,6
|
13,2
|
11,1
|
19,4
|
11,6
|
10,1
|
13,8
|
| Employés |
9,7
|
12,0
|
7,4
|
8,4
|
9,6
|
11,3
|
13,3
|
8,3
|
9,6
|
| Ouvrier |
17,3
|
33,0
|
17,3
|
31,7
|
26,8
|
38,0
|
39,3
|
35,0
|
29,5
|
| Personnel |
1,4
|
1,3
|
0,9
|
2,3
|
4,2
|
1,5
|
1,3
|
0,5
|
1,9
|
| Autres actif |
1,7
|
1,8
|
8,5
|
6,6
|
2,9
|
3,2
|
2,1
|
4,8
|
4,6
|
| Non actifs |
16,3
|
9,8
|
14,6
|
14,0
|
16,7
|
6,1
|
7,6
|
9,3
|
12,7
|
|
total
|
100,00
|
100,00
|
100,00
|
100,00
|
100,00
|
100,00
|
100,00
|
100,00
|
100,00
|
Tableau 3
Ce sont les tableaux 2 et 3 qui définiront les coordonnées dans les deux espaces (sous forme de fréquences et non de pourcentages : totaux de lignes ou colonnes égaux à 1 au lieu de 100).
Notations :
|
|
k =
|
 |
|
|
fij =
|
 |
|
|
fi. =
|
 |
|
|
f.j =
|
 |
• Dans l’espace Rp on construit un nuage de n points, chaque point i ayant pour coordonnées les quantités : {
; j=1, 2, ..., p} et étant affecté de la masse fi.
Ces n points seront situés dans un sous-espace à p-1 dimensions, leurs n coordonnées vérifiant la relation 
pour tout i=1, ..., n.
• Dans l’espace Rn on construit un nuage de p points, chaque point j ayant pour coordonnées les quantités : {
; i=1, 2, ..., n} et étant affecté de la masse f.j
Ces p points seront situés dans un sous-espace à n-1 dimensions, leurs p coordonnées vérifiant la relation 
pour tout j=1, ..., p.
• Les proximités entre les points s’interprètent alors en terme de proximités entre profils.
On choisit comme dimension de départ celle correspondant à la plus petite dimension du tableau. Dans l’exemple, on se placera dans Rn où n = 8.
Choix des distances
Pour travailler sur des profils, dans les espaces Rp et Rn on munit ces espaces d’une distance différente de la distance euclidienne usuelle : la distance du Chi-deux (distance pondérée).
La distance entre deux catégories socio-professionnelle i et i’ sera donnée par :
d2(i, i’) = 
(1)
La distance entre deux modes d’hébergement j et j’ sera :
d2(j, j’) = 
(2)
La distance du Chi-deux vérifie le principe d’équivalence distributionnelle.
Principe d’équivalence distributionnelle :
Si deux points-lignes i1 et i2 sont confondus dans Rp et si on les considère comme un seul point afffecté de la somme des masses de i1 et de i2 (remplacés par i0) alors les distances entre tous les couples de points dans Rp et dans Rn restent inchangés. Il en est de même pour deux points-colonne j1 et j2 de Rn ayant les mêmes propriétés. (:309)
Cette distance doit rendre " proches " des points de I dont les associations à J, dont les comportements sur J (donc les profils) sont voisins ou semblables. De même, cette distance fera paraître " éloignés " des points différant sensiblement selon J.
Les AFC sont réalisée par voie informatique. Les résultats délivrés par la machine comprennent les valeurs propres, pourcentages d’inertie, coordonnées factorielles et contributions relatives et absolues.
• Le support du nuage est un espace à n-1 = 8-1 = 7 dimensions.
• La trace de la matrice = 0,0839 (c’est la somme des valeurs propres autres que 1)
• Les valeurs propres interviennent par le biais du coefficient 
pour caractériser la qualité de la représentation simultanée.
La "valeur propre" représente, pour chaque facteur, le montant de l’inertie du nuage sur ce facteur par rapport à la somme de toutes les valeurs propres qui représente 100% de cette inertie.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 4 - Valeurs propres et pourcentages de variance des facteurs.
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
Hôtel
|
|
|
|
|
|
|
|
|
|
|
|
|
Location
|
|
|
|
|
|
|
|
|
|
|
|
|
Propriété
|
|
|
|
|
|
|
|
|
|
|
|
|
Parents
|
|
|
|
|
|
|
|
|
|
|
|
|
Amis
|
|
|
|
|
|
|
|
|
|
|
|
|
Tente
|
|
|
|
|
|
|
|
|
|
|
|
|
Village
|
|
|
|
|
|
|
|
|
|
|
|
|
Divers
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 5 - Paramètres des points-colonnes (Modes d’hébergement)
j ?= identificateur des variables
Masse ?= poids associé au point j = fj
jaj ?= coordonnée de la variable j sur l’axe de rang a
caaj ?= 
= contribution absolue de la variable j à la variance de l’axe a.
craj ?= contribution relative de a à l’inertie de j = 
= cosinus carré de l’angle formé par j et l’axe a = explication de la variable j par l’axe de rang a
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Tableau 5bis - Paramètres des points-lignes (Catégories socio-professionnelle)
i ?= identificateur des variables
Masse fi?= poids marginal associé au point i
yai ?= coordonnée de l’individu i sur l’axe de rang a
caai ?= 
= contribution absolue de l’individu i à la variance de l’axe a.
crai ?= contribution relative de a à l’excentricité de i = 
= cosinus carré de l’angle formé par i et l’axe a = explication de l’individu i par l’axe de rang a
Elles expriment la part prise par un élément donné dans la variance expliquée par un facteur. Elles permettent de savoir quelles variables interviennent fortement dans la construction d’un facteur.
mesure la part de l’élément i dans la variance expliquée de l’axe a. Nous aurons 
La contribution absolue de l’élément j à l’axe a est 
Les points ayant de fortes contributions absolues sur un axe a sont ceux qui contribuent à définir la signification de cet axe factoriel. Ce sont les points explicatifs de l’axe.
Elles expriment la part prise par un facteur dans l’explication de la dispersion d’un élément.
. C’est le carré du cosinus du point i avec l’axe a. Il s’interprète comme le carré d’un coefficient de corrélation.
La contribution relative de l’élément j à l’axe a est 
.
G et H sont les centres de gravité des nuages de points en Rp et Rn ; d est la distance du point i au centre de gravité.
Les points ayant de fortes contributions relatives sur un axe a sont les points expliqués de l’axe.
L’un des intérêts de l’AFC est de permettre une représentation graphique des nuages de points I et J dans un espace de faible dimension, permettant de mettre en évidence des éléments (correspondances) que le calcul numérique ne permet pas d’apprécier instantanément.
Traditionnellement, la représentation se fait en 2 dimensions, en traçant successivement les plans factoriels F1/F2, F1/F3 et F2/F3 (et plus, si davantage de facteurs sont requis dans l’interprétation).
Pour les représentations, les coordonnées sont celles calculées au § 4.3.
Les proximités observables sur le premier plan factoriel sont schématisées sur la figure 1.
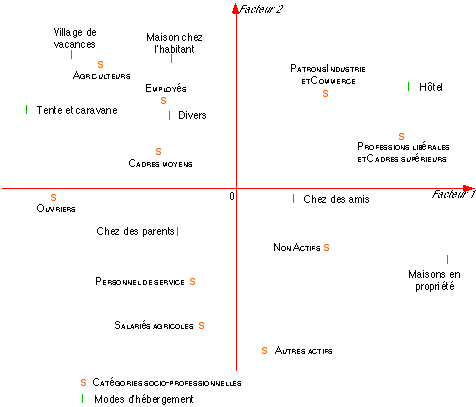
Figure 1
La proximité entre deux points-lignes (catégories socio-professionnelles) traduit une similitude des profils d’hébergement (ex: " patrons " et " professions libérales ").
La proximité entre deux points-colonnes (modes d’hébergement) traduit une similitude des profils socio-professionnels (ex : " village vacance " et " tentes & caravanes ").
La représentation simultanée des points lignes et des points colonnes permet d’identifier les variables responsables de certaines proximités.
Les proximités entre profils s’interprètent par référence au profil moyen. Les proximités sont plus aisées à interpréter à la périphérie du graphique.
Les variables responsables de la construction des axes (contributions absolues fortes) sont pour le premier axe : " Hôtel ", " Maisons en propriété " et " Tentes/caravanes " (qui expliquent 88% de la variance). L’hébergement " Village de vacance " participe peu car sa masse est 3 fois plus faible que " Tente-caravane ". Pour l’axe 2, l’hébergement " Chez des parents " a une forte contribution (41,7) alors que " Maison en propriété " n’est que de 6,1.
Pour les catégories socio-professionnelles, " Cadres sup " et " Ouvrier " définissent le premier axe (73%). En raison de leurs contributions relatives, ces deux catégories ne caractérisent que ce premier axe.
Le graphique doit être lu à la clarté des tableaux qui permettent de nuancer son interprétation.
1. Les axes factoriels relatifs aux plus grandes valeurs propres sont ceux qui discriminent le plus les points des nuages car, dans les directions de ces axes, l’inertie est la plus grande. Tous les axes factoriels sont, par construction, orthogonaux, c’est à dire non corrélés deux à deux.
2. Pour interpréter un axe, il faut examiner les extrêmes selon cet axe et exprimer, en langage clair, la raison de l’opposition, en intégrant tous les points, en particulier ceux qui ont une contribution absolue importante. Ceci amène à ne pas tenir compte de certains points très " légers ", éloignés sur les axes.
3. Un premier facteur qui représenterait 10% de l’inertie totale serait très significatif, dans l’étude d’un questionnaire, par exemple.
4. Lorsque l’on passe d’un taux d’inertie donné pour un facteur à un taux d’inertie nettement plus faible pour le facteur suivant, le premier cité a généralement un sens clair.
5. Il vaut mieux examiner un facteur sur un plan que sur un axe. Il est prudent de se méfier de l’association étroite que l’on accorderait à deux points i et j à la vue d’un seul plan factoriel. Cette proximité sur un plan peut être contredite par des coordonnées très différentes (signe opposé) sur une autre facteur (i.e. : ne pas se contenter d’examiner le plan F1F2, envisager également F1F3 et F2F3).
Le tableau ci-dessous représente le nombre de dépôts de brevets en télécommunication dans 9 pays, au cours des années 1980 à 1986.
|
|
|
|
|
|
|
|
|
| USA |
986
|
774
|
711
|
591
|
467
|
404
|
258
|
|
Japon
|
653
|
552
|
361
|
307
|
195
|
129
|
43
|
|
RFA
|
405
|
357
|
347
|
254
|
294
|
313
|
208
|
|
France
|
189
|
158
|
200
|
171
|
153
|
184
|
147
|
|
GB
|
204
|
182
|
158
|
137
|
92
|
86
|
67
|
|
Italie
|
31
|
28
|
28
|
21
|
22
|
29
|
15
|
|
Pays-Bas
|
64
|
59
|
61
|
64
|
33
|
30
|
11
|
|
Suède
|
25
|
19
|
31
|
25
|
15
|
12
|
13
|
|
Suisse
|
23
|
34
|
19
|
30
|
17
|
30
|
15
|
Le tableau des valeurs propres réunit :
• Le numéro d’ordre des valeurs propres classées par ordre décroissant (a = 2, ..., p) [l1= 1 : la première valeur propre est égale à 1 et n’intervient pas dans l’analyse]
• le nombre d’itération par facteur pour obtenir les résultats numériques
• les valeurs propres (autres que 1) la de la matrice diagonalisée. La somme des valeurs propres, ou trace de la matrice, est exprimée en bas du tableau = 
• le pourcentage d’inertie de chaque axe factoriel a = 
• les pourcentages d’inertie cumulés.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
La première valeur propre représente un très grand pourcentage de la varaince totale. C’est un cas d’école!
Les coordonnées factorielles des points variables j sont données par la formule
où 
est la ième composante du vecteur propre 
de la matrice S*=YY’.
Les coordonnées factorielles des points variables j sont publiées dans le tableau suivant :
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1
|
1986
|
1000
|
223
|
183
|
190
|
958
|
197
|
-28
|
23
|
69
|
13
|
4
|
26
|
||||||
|
2
|
1985
|
1000
|
187
|
135
|
171
|
882
|
133
|
-35
|
40
|
90
|
-48
|
71
|
302
|
||||||
|
3
|
1984
|
1000
|
166
|
17
|
10
|
20
|
0
|
44
|
428
|
118
|
47
|
479
|
251
|
||||||
|
4
|
1983
|
999
|
138
|
40
|
26
|
50
|
2
|
107
|
858
|
569
|
-26
|
53
|
67
|
||||||
|
5
|
1982
|
999
|
111
|
51
|
-127
|
779
|
45
|
-34
|
57
|
48
|
56
|
148
|
239
|
||||||
|
6
|
1981
|
1001
|
106
|
240
|
-315
|
955
|
258
|
-51
|
26
|
103
|
-7
|
1
|
5
|
||||||
|
7
|
1980
|
999
|
68
|
335
|
-468
|
969
|
365
|
9
|
0
|
2
|
-47
|
10
|
110
|
||||||
|
1000
|
1000
|
1000
|
1000
|
||||||||||||||||
où :
n ?= numéro d’ordre des variables
j ?= identificateur des variables
qlts(j) ?=Qualité d’explication du point j dans l’espace factoriel composé de s facteurs.
pds ?= poids associé au point j = fj
inr ?= pourcentage d’inertie de chaque point j par rapport à l’inertie totale du nuage = fj-r2(j)/M2(N(J)) ; r(j) = excentricité du point j.
jaj ?= coordonnée de la variable j sur l’axe de rang a.
coraj ?= contribution relative de a à l’inertie de j = = cosinus carré de l’angle formé par j et l’axe a = explication de la variable j par l’axe de rang a.
ctraj ?= = contribution absolue de la variable j à la variance de l’axe a.
1. Points explicatifs
Les points explicatifs de l’axe permettent d’interpréter la signification du facteur considéré. Il s’agit des points ayant, pour les coordonnées positives et pour les coordonnées négatives, les plus fortes valeurs de contribution ctraj.
Ici, il s’agit de :
|
coordonnées négatives
|
coordonnées positives
|
|
|
axe 1
|
1980 (365)
1981 (258) |
1986 (197)
|
|
axe 2
|
1981
|
1983 (569)
|
|
axe 3
|
néant
|
néant
|
2. Points expliqués
Ce sont ceux dont la contribution relative à l’excentricité coraj est forte, c’est-à-dire supérieure à un seuil défini, ici 500. Ces points sont :
|
coordonnées négatives
|
coordonnées positives
|
|
|
axe 1
|
1980 (969)
1981 (955) |
1986 (958)
1985 (882) |
|
axe 2
|
néant
|
1983 (569)
|
Il n’y a pas de points expliqués pour l’axe 3.
3. Interprétation
L’axe 1 définit une croissance des dépôts de brevet entre les années de début (1980, 81) et la fin (1986), avec une forte contribution des années 80, 81, 85 et 86.
L’axe 2 fait ressortir l’importance de l’année 1983.
L’axe 3 traduit l’opposition entre les années 82/84 et 85.
Les coordonnées factorielles des points individus i sont données par la formule
où 
est la ième composante du vecteur propre 
de la matrice T*=YY’.
Les coordonnées factorielles des points individus i sont publiées dans le tableau suivant :
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1
|
USA
|
1000
|
363
|
18
|
39
|
681
|
14
|
12
|
65
|
19
|
20
|
183
|
103
|
||||||||
|
2
|
Japo
|
1000
|
194
|
431
|
318
|
988
|
478
|
-28
|
8
|
60
|
-19
|
4
|
54
|
||||||||
|
3
|
RFA
|
100
|
189
|
183
|
-198
|
891
|
183
|
-65
|
98
|
299
|
15
|
5
|
30
|
||||||||
|
4
|
F
|
100
|
104
|
232
|
-317
|
983
|
256
|
36
|
12
|
48
|
-8
|
1
|
6
|
||||||||
|
5
|
GB
|
1000
|
80
|
8
|
24
|
134
|
1
|
40
|
365
|
47
|
-33
|
259
|
64
|
||||||||
|
6
|
Ital
|
1001
|
15
|
19
|
-212
|
798
|
17
|
-63
|
71
|
22
|
10
|
2
|
1
|
||||||||
|
7
|
NL
|
1000
|
28
|
31
|
86
|
144
|
5
|
172
|
571
|
298
|
16
|
5
|
5
|
||||||||
|
8
|
Suè
|
999
|
12
|
17
|
-100
|
153
|
3
|
216
|
702
|
205
|
57
|
49
|
27
|
||||||||
|
9
|
CH
|
1000
|
15
|
61
|
-338
|
627
|
43
|
22
|
3
|
3
|
-258
|
365
|
709
|
||||||||
|
1000
|
1000
|
1000
|
1000
|
||||||||||||||||||
où :
n = numéro d’ordre des variables
i = identificateur des variables
qlts(i) ?= Qualité d’explication du point i dans l’espace factoriel composé de s facteurs, qlts(i) = 
pds ?= poids marginal associé au point j = fi
inr ?= pourcentage d’inertie de chaque point i par rapport à la variance totale du nuage M2(N(I)) = fi-r2(i)/M2(N(I)) ; r(i) = excentricité du point i ;
yai ?= coordonnée de l’individu i sur l’axe de rang a
corai ?= contribution relative de a à l’excentricité de i = = cosinus carré de l’angle formé par i et l’axe a = explication de l’individu i par l’axe de rang a
ctrai ?= = contribution absolue de l’individu i à la variance de l’axe a.
1. Points explicatifs
Ce sont les points dont la contribution relative à la variance de l’axe a est prépondérante. Il s’agit des points ayant, pour les coordonnées positives et pour les coordonnées négatives, les plus fortes valeurs de contribution ctra(i).
Ici, il s’agit de :
|
coordonnées négatives
|
coordonnées positives
|
|
|
axe 1
|
France (256)
RFA (183) |
Japon (478)
|
|
axe 2
|
RFA (299)
|
NL (298)
Suède (205) |
|
axe 3
|
Suisse CH (709)
|
Néant
|
C’est sur ces points que doit s’appuyer l’interprétation de l’axe factoriel correspondant.
2. Points expliqués
Ce sont ceux dont la contribution relative à l’excentricité cora(i) est forte, c’est-à-dire supérieure à un seuil défini, ici 500. Ces points sont :
|
coordonnées négatives
|
coordonnées positives
|
|
|
axe 1
|
France (983)
RFA (891) Italie (798) Suisse (627) |
Japon (988)
USA (681) |
|
axe 2
|
néant
|
NL (571)
Suède (702) |
|
axe 3
|
Néant
|
Néant
|
Il n’y a pas de points expliqués pour l’axe 3.
3. Interprétation
L’axe 1 oppose la forte croissance du Japon et des USA à la faible croissance de la RFA et de la France.
L’axe 2 oppose les effets d’intensité de NL et Suède qui doublent leurs dépots.
Elle correspond à la somme des pourcentages de variance des s axes considérés comme interprétables. Voir le tableau § 442. Ici, nous aurons pour
|
le facteur F1
|
88.998
|
89 %
|
|
les facteurs F1 et F2
|
94.993
|
95 %
|
|
les facteurs F1, F2 et F3
|
98.158
|
98 %
|
... de la variance totale expliquée. Généralement on se contente de 80 % d’explication totale de la variance. Les très fortes valeurs obtenues dans cet exemple montrent le caractère trivial des facteurs mis en évidence.
Pour chaque point individu et chaque pont variable, il est possible de calculer une qualité d’explication dans un espace factoriel de rang défini (s) :
qlts (i) =
et qlts (j) = 
|
I\ qlt
|
qlt1
|
qlt2
|
qlt3
|
J\ qlt
|
qlt1
|
qlt2
|
qlt3
|
|
USA
|
681
|
746
|
929
|
1986
|
958
|
981
|
985
|
|
Japon
|
988
|
996
|
1000
|
1985
|
882
|
922
|
993
|
|
RFA
|
891
|
989
|
994
|
1984
|
20
|
448
|
927
|
|
France
|
983
|
995
|
996
|
1983
|
50
|
908
|
961
|
|
GB
|
134
|
499
|
758
|
1982
|
779
|
836
|
984
|
|
Italie
|
798
|
869
|
871
|
1891
|
995
|
981
|
982
|
|
Pays Bas
|
144
|
715
|
720
|
1980
|
969
|
969
|
979
|
|
Suède
|
153
|
855
|
904
|
||||
|
Suisse
|
627
|
630
|
995
|
La représentation peut se faire séparément pour chacun des ensemble I et J ou sur le même système d’axes. Dans le cas de très grands tableaux, seuls les points explicatifs et expliqués seront représentés.
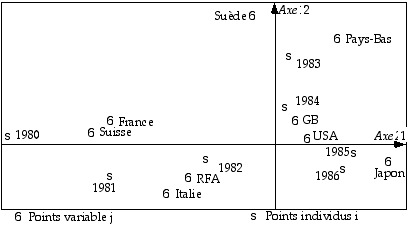
Représentation des points i de N(I) et j de N(J) dans l’espace factoriel (1, 2).
Représentation des points i de N(I) et j de N(J) dans l’espace factoriel (1, 3).